Cách Xác Định Thiết Diện Trong Hình Học Không Gian
Cách tra cứu thiết diện vào hình học không gian rất hay
Với Cách tra cứu thiết diện trong hình học tập không khí cực tuyệt Toán thù lớp 11 bao gồm tương đối đầy đủ phương thức giải, ví dụ minc họa cùng bài bác tập trắc nghiệm tất cả giải mã chi tiết để giúp học sinh ôn tập, biết cách làm dạng bài bác tập tìm kiếm tiết diện vào hình học tập không gian từ bỏ đó đạt điểm trên cao trong bài xích thi môn Toán thù lớp 11.
Bạn đang xem: Cách xác định thiết diện trong hình học không gian

A. Pmùi hương pháp giải
Để xác minh thiết diện của khía cạnh phẳng (α) đi qua điểm O với vuông góc với đường thẳng d với cùng 1 hình chóp ta triển khai theo 1 trong hai phương pháp sau:
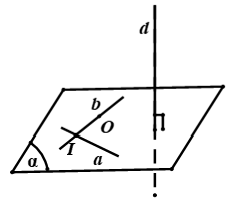
Cách 1. Tìm tất cả những con đường thẳng vuông góc cùng với d, khi ấy (α) đã tuy nhiên song hoặc chứa các mặt đường trực tiếp này cùng ta đưa về dạng thiết diện tuy vậy song như đang biết sinh hoạt cmùi hương II.
Cách 2. Ta dựng khía cạnh phẳng (α) nhỏng sau:
Dựng hai tuyến đường trực tiếp a; b cắt nhau cùng vuông góc cùng với d trong số ấy gồm một mặt đường thẳng trải qua O, lúc ấy (α) chính là mặt phẳng (a; b)
B. Ví dụ minch họa
lấy một ví dụ 1: Cho hình chóp S.ABCD bao gồm lòng ABC là tam giác đông đảo, SA ⊥ (ABC). điện thoại tư vấn (P) là khía cạnh phẳng qua B cùng vuông góc cùng với SC. Thiết diện của (P) cùng hình chóp S.ABC là:
A. Hình thang vuông.
B. Tam giác phần lớn.
C. Tam giác cân.
D. Tam giác vuông.
Hướng dẫn giải
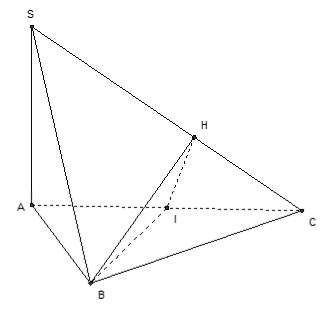
điện thoại tư vấn I là trung điểm của CA, kẻ IH ⊥ SC.
Ta tất cả BI ⊥ AC, BI ⊥ SA ⇒ BI ⊥ SC
Do kia SC ⊥ (BIH) xuất xắc thiết diện là tam giác BIH.
Mà BI ⊥ (SAC) nên BI ⊥ IH giỏi thiết diện là tam giác vuông.
Chọn D
Ví dụ 2: Cho tứ đọng diện các ABCD cạnh a = 12, hotline (P) là mặt phẳng qua B cùng vuông góc cùng với AD. Thiết diện của (P) và hình chóp bao gồm diện tích bằng
A. 36√2B. 40C. 36√3D. 36
Hướng dẫn giải
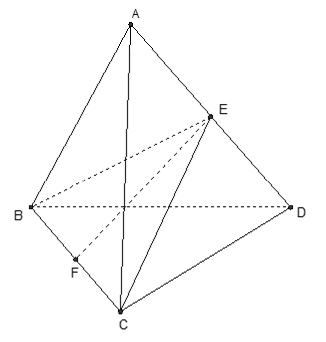
điện thoại tư vấn E là trung điểm AD
Do tam giác ABD đầy đủ buộc phải BE ⊥ AD(1)
Do tam giác ACD phần nhiều yêu cầu CE ⊥ AD(2)
Từ (1) với (2) suy ra: AD ⊥ (BEC)
⇒ Thiết diện là tam giác BCE. hotline F là trung điểm của BC.
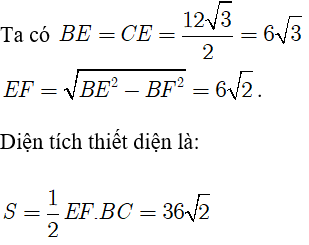
Chọn A
Ví dụ 3: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , sát bên SA ⊥ (ABC) Mặt phẳng (P) đi qua trung điểm M của AB cùng vuông góc cùng với SB giảm AC, SC, SB theo lần lượt trên N, Phường, Q . Tứ đọng giác MNPQ là hình gì ?
A. Hình thang vuông
B. Hình thang cân
C. Hình bình hành
D. Hình chữ nhật
Hướng dẫn giải
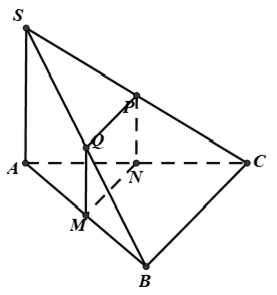
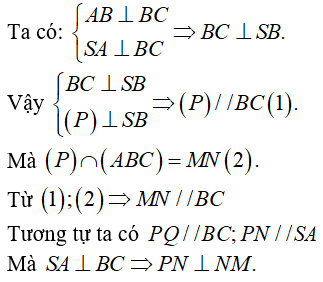
Vậy thiết diện là hình thang MNPQ vuông trên N
Chọn A
lấy một ví dụ 4: Cho hình chóp S.ABC tất cả đáy ABC là tam giác mọi, O là trung điểm của con đường cao AH của tam giác ABC. SO vuông góc cùng với lòng. hotline I là điểm tùy ý bên trên OH (không trùng cùng với O với H). phương diện phẳng (P) qua I với vuông góc với OH. Thiết diện của (P) cùng hình chóp S.ABC là hình gì?
A. Hình thang cân
B. Hình thang vuông
C. Hình bình hành
D. Tam giác vuông
Hướng dẫn giải
+ Mặt phẳng (P) vuông góc với OH đề xuất (P) // SO
Suy ra (P) cắt (SAH) theo giao tuyến là đường thẳng
Qua I và tuy nhiên tuy vậy với SO cắt SH tại K.
Xem thêm: Cách Dùng Mail Merge Trong Word 2013, Sử Dụng Mail Merge, Cách Trộn Thư (Mail Merge) Trong Word
+ Từ giả thiết suy ra (P) // BC, bởi vì đó (P) sẽ cắt (ABC) và (SBC) lần lượt là các đường thẳng qua I và K tuy vậy song với BC cắt AB, AC, SB, SC lần lượt tại M, N, P, Q
Do đó thiết diện là tứ giác MNPQ.
+ Ta có MN và PQ cùng song song BC suy ra I là trung điểm của MN và K là trung điểm của PQ.
Lại có các tam giác ABC đều và tam giác SBC cân tại S suy ra IK vuông góc với MN và PQ dó đó MNPQ là hình thang cân.
Chọn đáp án A.
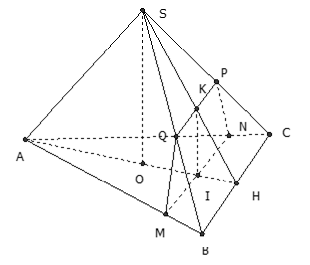
lấy ví dụ như 5: Cho hình chóp S.ABC tất cả lòng ABC là tam giác rất nhiều cạnh a với SA = SB = SC = b (a > b√2). Call G là trọng tâm . Xét khía cạnh phẳng (P) trải qua A với vuông góc với SC trên điểm C1 nằm giữa S cùng C. Diện tích tiết diện của hình chóp lúc giảm bởi vì khía cạnh phẳng (P) là
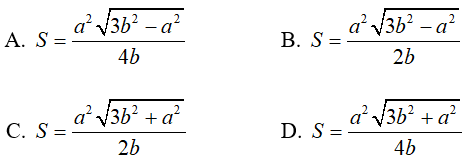
Hướng dẫn giải
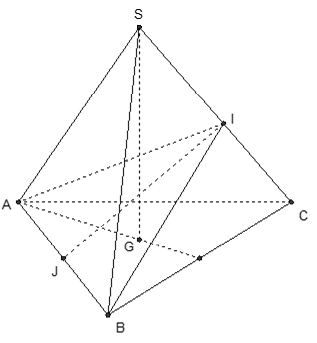
Kẻ AI ⊥ SC ta có: ΔSAC = ΔSBC (c.c.c) đề xuất hai tuyến phố cao khớp ứng đều nhau.
⇒ BI ⊥ SC
⇒ (AIB) ⊥ SC. Thiết diện là tam giác AIB.
Ta có
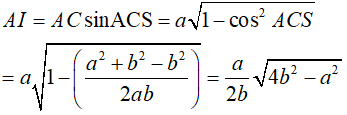
Gọi J là trung điểm của AB. Dễ thấy tam giác AIB cân trên I, suy ra IJ ⊥ AB .
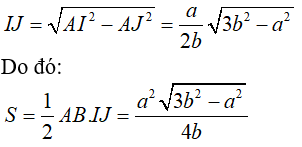
Chọn A
ví dụ như 6: Tam giác ABC có BC = 2a, đường cao AD = a√2. Trên con đường trực tiếp vuông góc với (ABC) tại A, đem điểm S sao cho SA = a√2. Hotline E; F theo thứ tự là trung điểm của SB và SC . Diện tích tam giác AEF bằng?
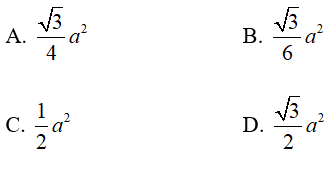
Hướng dẫn giải
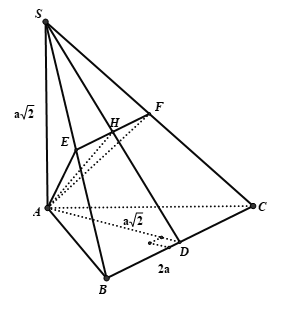

lấy ví dụ 7: Cho hình chóp S. ABC gồm đáy ABC là tam giác các, SA ⊥ (ABC). Hotline (P) là mặt phẳng qua B và vuông góc với SC. Thiết diện của (P) và hình chóp S.ABC là:
A. Hình thang vuông
B. Tam giác đều
C. Tam giác cân
D. Tam giác vuông
Hướng dẫn giải
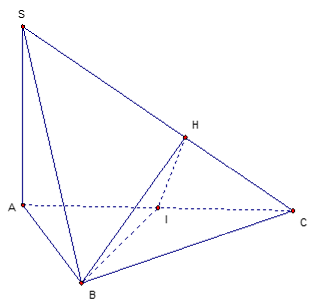
+ gọi I là trung điểm của AC, kẻ IH ⊥ SC
Ta có BI ⊥ AC, BI ⊥ SA ⇒ BI ⊥ (SAC)
⇒ BI ⊥ SC. Mà IH ⊥ SC
Do kia SC ⊥ (BIH) hay thiết diện là tam giác BIH .
+ Mà BI ⊥ (SAC) đề xuất BI ⊥ IH xuất xắc thiết diện là tam giác vuông.
Chọn D.
Xem thêm: Cách Đổi Tiếng Việt Trên Máy Tính, Cách Để Đổi Ngôn Ngữ Trên Máy Tính

C. các bài luyện tập vận dụng
Câu 1: Cho hình chóp S.ABC bao gồm đáy ABC là tam giác phần nhiều cạnh 2a, SA ⊥ (ABC), SA = a(√3/2). Call (P) là phương diện phẳng đi qua A và vuông góc với BC. Thiết diện của hình chóp S.ABC được giảm vị (P) gồm diện tích S bằng?

Lời giải:
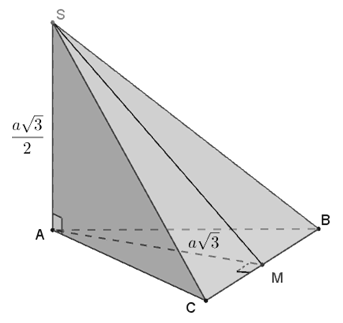
Hotline M là trung điểm của BC thì BC ⊥ AM (1)
Hiển nhiên AM = a√3.
Mà SA ⊥ (ABC) ⇒ BC ⊥ SA(2)
Từ (1) cùng ( 2) suy ra BC ⊥ (SAM) ⇒ (P) ≡ (SAM)
Lúc đó tiết diện của hình chóp S.ABC được giảm vì (P) chính là tam giác SAM
Do tam giác SAM vuông tại A phải
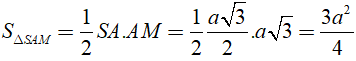
Chọn lời giải C
Câu 2: Cho hình chóp S.ABC gồm lòng ABC là tam giác rất nhiều cạnh a, SA ⊥ (ABC), SA = a. điện thoại tư vấn (P) là khía cạnh phẳng trải qua S cùng vuông góc cùng với BC. Thiết diện của (P) và hình chóp S.ABC gồm diện tích bởi ?
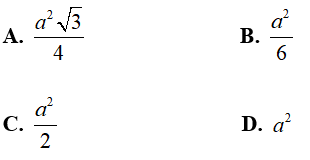
Lời giải:
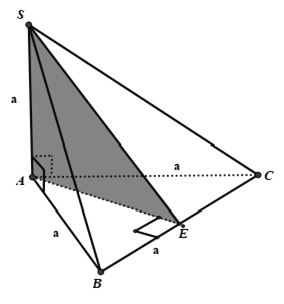
Kẻ AE ⊥ BC, SA ⊥ BC ⇒ BC ⊥ (SAE) ≡ (P)
Thiết diện của khía cạnh phẳng (P) cùng hình chóp S.ABC là tam giác SAE.
Tam giác SAE vuông tại A vị SA ⊥ (ABC), có:
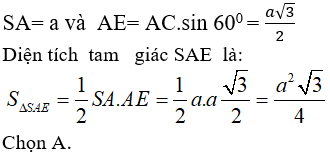
Câu 3: Cho tứ diện SABC có hai khía cạnh (ABC) cùng (SBC) là nhì tam giác phần lớn cạnh a, SA = a(√3/2). M là vấn đề trên AB làm thế nào cho AM = b ( 0



















