KHOẢNG CÁCH TỪ ĐIỂM ĐẾN MẶT PHẲNG TRONG KHÔNG GIAN

trangnhacaiuytin.com reviews đến những em học viên lớp 12 nội dung bài viết Phương pháp tính khoảng cách xuất phát điểm từ một điểm đến một mặt phẳng, nhằm giúp các em học tốt công tác Tân oán 12.

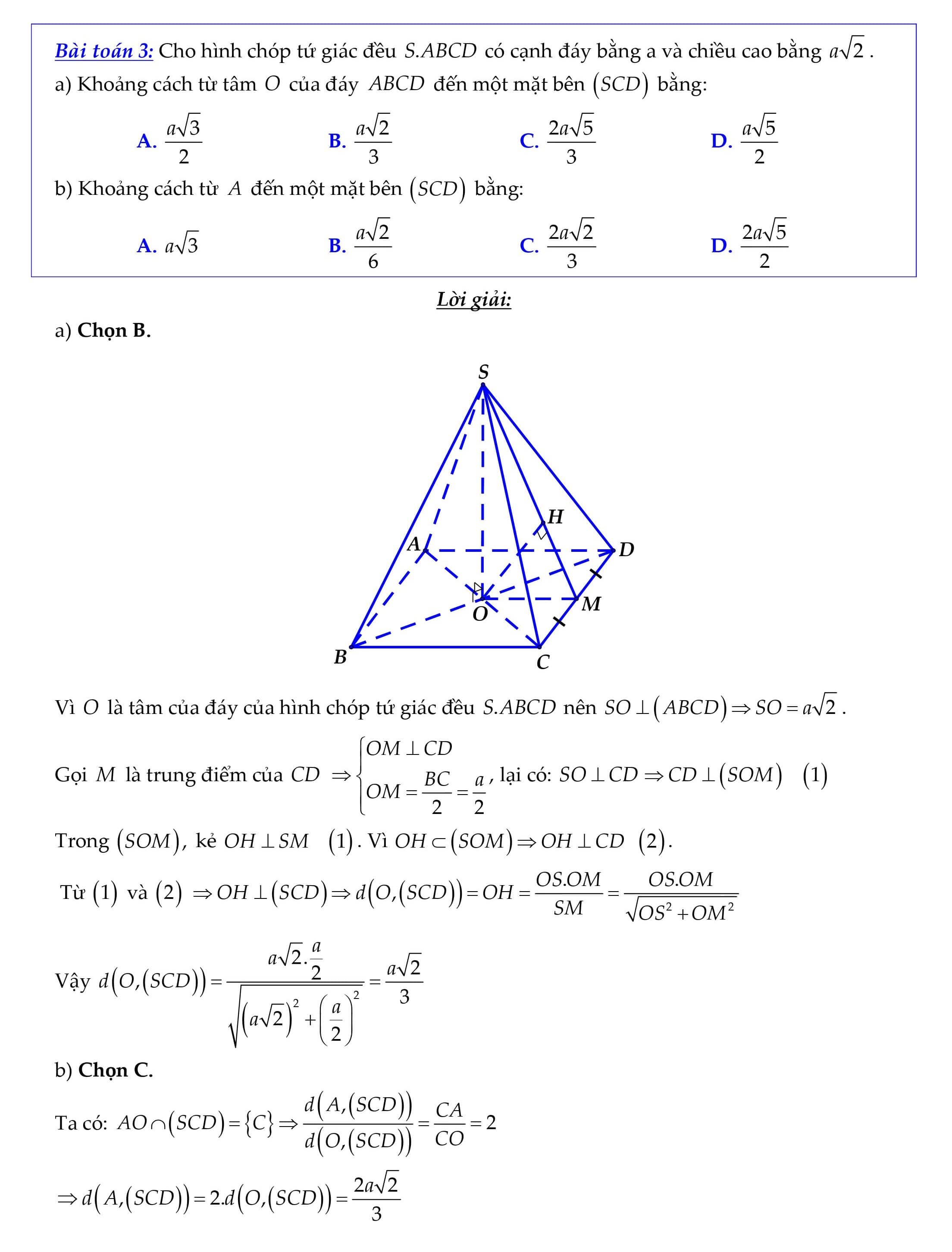
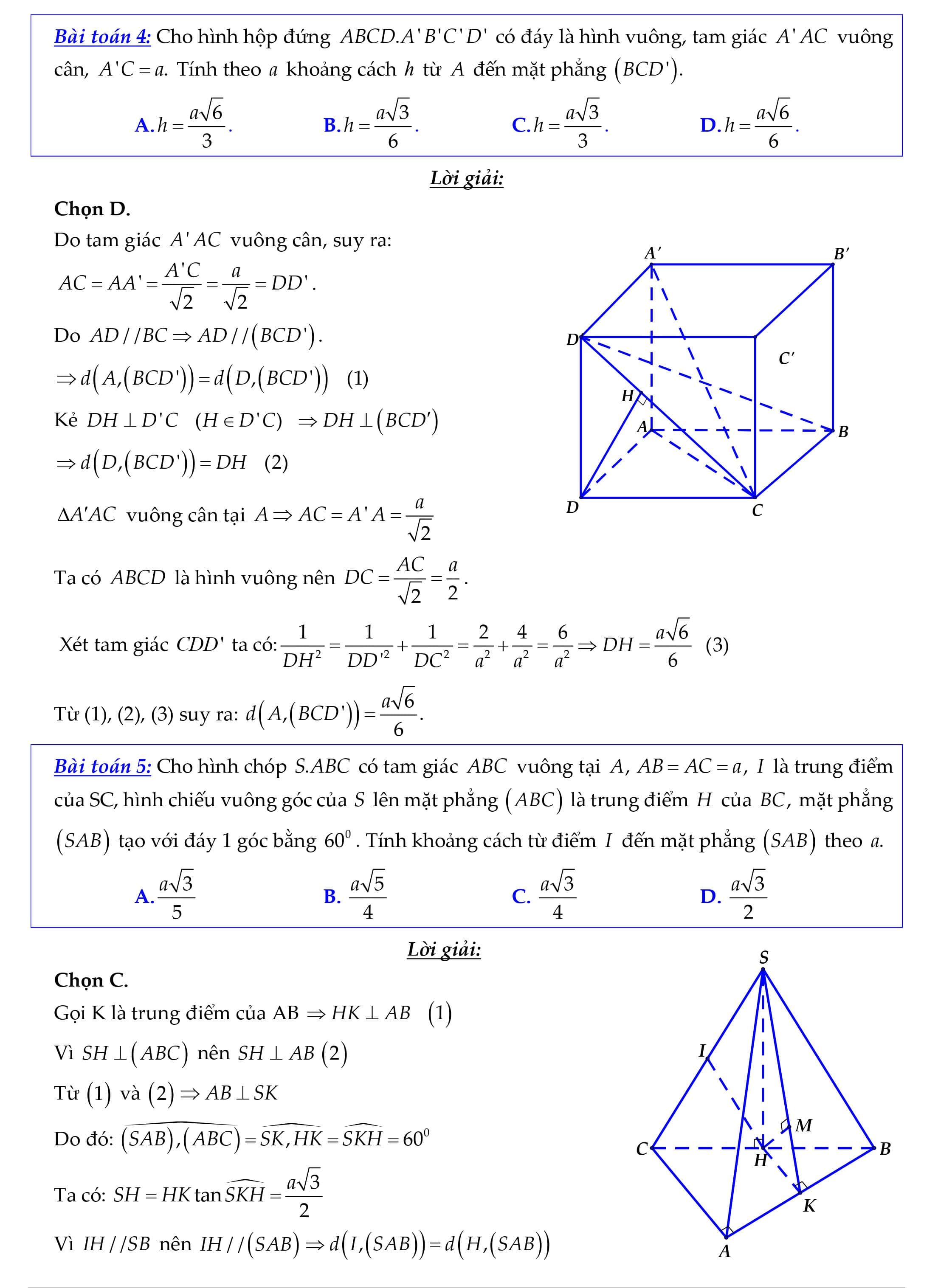
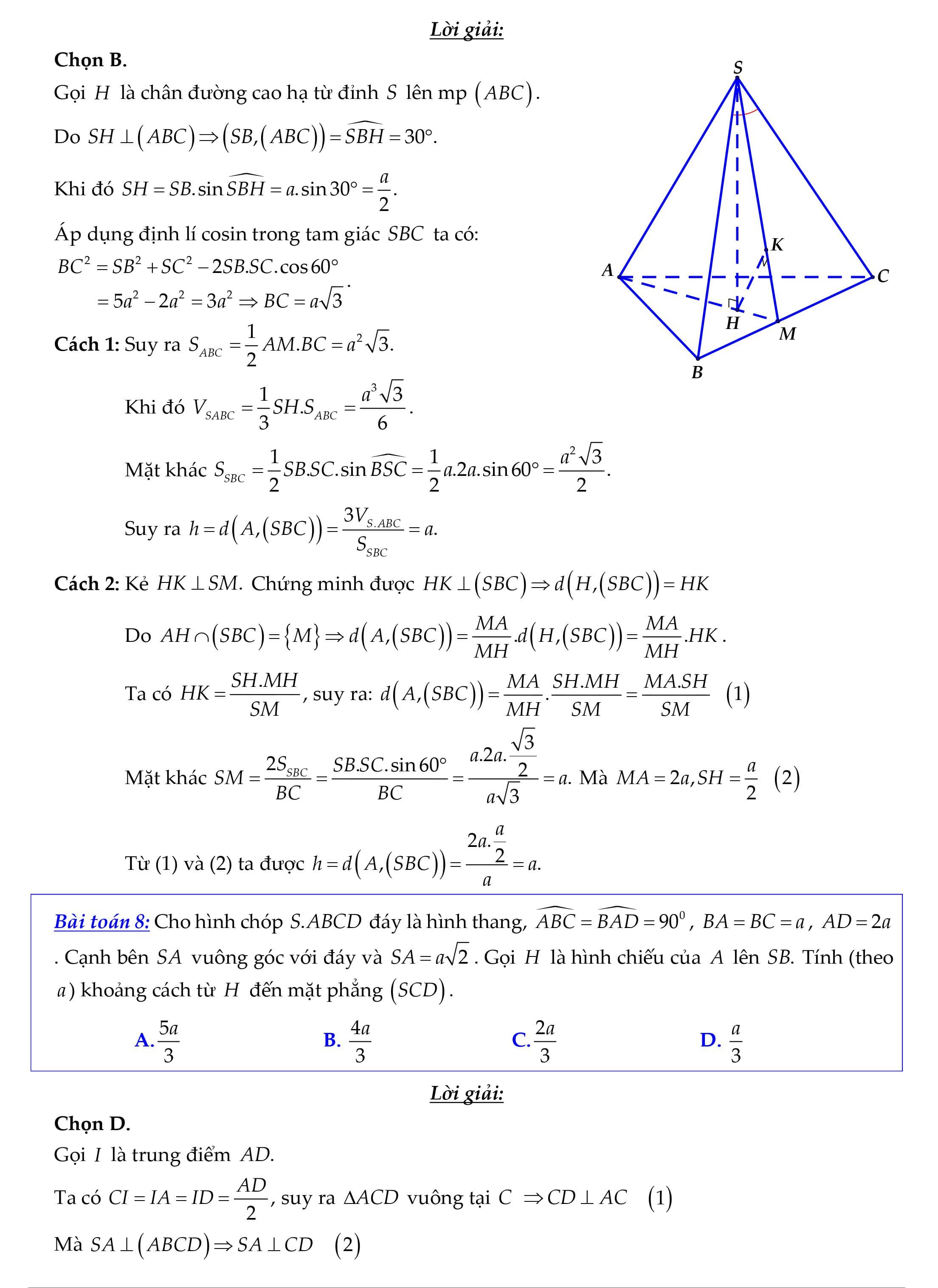
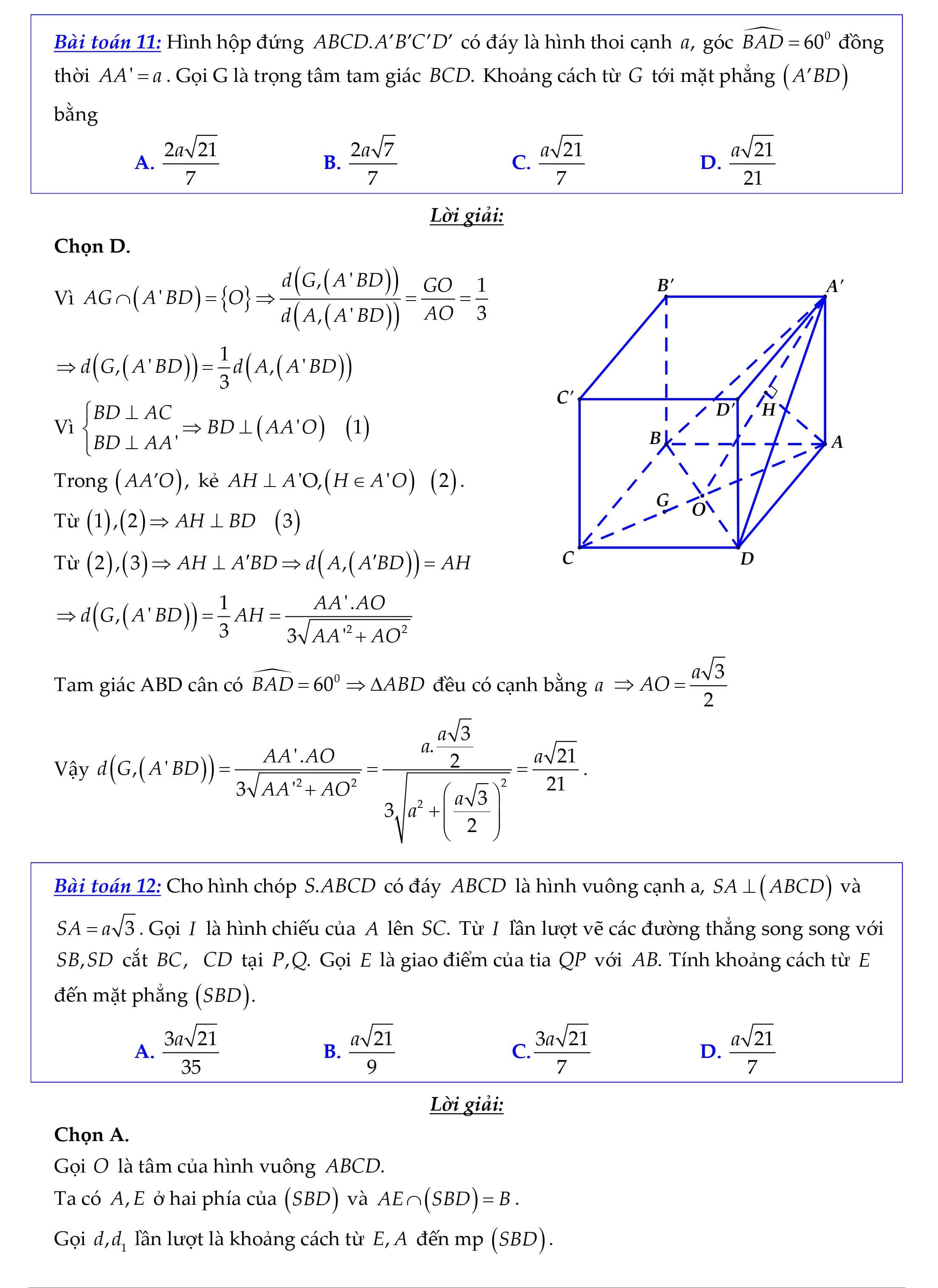
Nội dung nội dung bài viết Phương thơm pháp tính khoảng cách từ một điểm đến một mặt phẳng:KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT MẶT PHẲNG Nhắc lại: Khoảng cách từ bỏ điểm M mang đến khía cạnh phẳng (d) là MH , cùng với H là hình chiếu của M xung quanh phẳng (d). Kí hiệu: PHƯƠNG PHÁPhường. Bài toán: Tìm khoảng cách trường đoản cú điểm 0 mang lại mặt phẳng (a). do đó, mong mỏi tìm kiếm khoảng cách xuất phát từ 1 điểm đến chọn lựa một mặt phẳng, đầu tiên ta phải tìm hình chiếu vuông góc của đặc điểm này trên mặt phẳng. Việc xác minh hình chiếu của điểm cùng bề mặt phẳng ta thường được sử dụng một trong các phương pháp sau: Cách 1: Cách 1. Tìm hình chiếu H của 0 lên (a). Tìm khía cạnh phẳng (8) qua 0 oà vuông góc cùng với (a). Tìm A = (a) (B). Trong phương diện phẳng (8), kẻ OH IA tại H. PH là hình chiếu vuông góc của O lên (a). Cách 2. lúc đó OH là khoảng cách từ bỏ 0 mang lại (a). Lưu ý: Chọn khía cạnh phẳng (8) làm sao cho dễ tìm giao tuyến đường với (a). Cách 2: Nếu đã bao gồm trước đường thẳng d (a) thì kẻ Ox giảm (a) tại H.

Xem thêm: Cách Làm Bò Xào Hành Tây Ngon Tuyệt Cú Mèo, Cách Làm Thịt Bò Xào Hành Tây Nhanh


Xem thêm: Quy Tắc Về Cách Đeo Đồng Hồ Nam Đúng Cách Đeo Đồng Hồ Sao Cho Đúng Đẹp


Lúc đó, H là hình chiếu Ouông góc của.Một số chăm chú cùng thủ thuật giải khoảng cách quan trọng: Crúc ý đến sự việc chuyển bài toán thù search khoảng cách xuất phát từ một điểm (đề bài bác đến ngẫu nhiên cho một phương diện phẳng về bài toán thù tìm khoảng cách từ bỏ chân con đường cao đến phương diện phẳng đó với kiếm tìm côn trùng tương tác thân nhì khoảng cách này. Từ kia suy ra được khoảng cách theo trải nghiệm của đề bài bác. Khối hận chóp gồm những cạnh bên bởi nhau: Cho hình chóp bao gồm đỉnh S có các bên cạnh tất cả độ nhiều năm bởi nhau: SA = SB = SC = SD. khi kia hình chiếu 0 của S lên phương diện phẳng lòng trùng với tâm đường tròn nội tiếp đi qua các đỉnh ( A, B, C, D,…) vị trí mặt dưới. Nếu lòng là: Tam giác đa số, O là giữa trung tâm. Tam giác vuông, O là trung điểm cạnh huyền. Hình vuông, hình chữ nhật, O là giao điểm của 2 con đường chéo bên cạnh đó là trung điểm mỗi mặt đường. Sử dụng cách thức thể tích nhằm tìm khoảng tầm cách: Đưa bài bác tân oán khoảng cách về bài bác toán thù tra cứu độ cao của khối hận nhiều diện mà lại kân hận nhiều diện đó rất có thể xác minh được dễ ợt thể tích và mặc tích đáy. Phương pháp này được sử dụng trong ngôi trường hòa hợp chẳng thể tính được khoảng cách bằng cách vẻ ngoài tính tân oán như: định lí Pytago, các hệ thức lượng vào tam giác vuông, định lý cô-sin.Các bài bác tân oán tính khoảng cách từ là 1 điểm đến lựa chọn phương diện phẳng hay chạm mặt. Khoảng bí quyết từ chân mặt đường cao tới phương diện bên. Bài toán: Cho hình chóp bao gồm đỉnh S tất cả hình chiếu vuông góc lên mặt đáy là H. Tính khoảng cách tự điểm H mang đến khía cạnh mặt (SAB). Khoảng phương pháp từ một điểm bên trên dưới đáy tới phương diện đứng (chứa con đường cao). Bài toán: Cho hình chóp có đỉnh S có hình chiếu vuông góc lên mặt dưới là H. Tính khoảng cách tự điểm A bất kì đến phương diện mặt (SHB).