Cách Rút Gọn Biểu Thức Chứa Căn

Hướng dẫn giải pháp rút gọn biểu thức chứa căn mang đến học sinh lớp 9. Đây là dạng tân oán chắc chắn bao gồm trong số đề thi tuyển sinh vào lớp 10 môn Toán thù.

Bạn đang xem: Cách rút gọn biểu thức chứa căn

Để giải được bài tập rút ít gọn và tính giá trị của biểu thức chứa căn bậc hai họ cần ôn lại lý thuyết căn thức bậc nhì. Tức là:

Biến đổi biểu thức chứa căn bậc hai

Vận dụng các quy tắc dưới đây:

1. Đưa thừa số ra ngoài dấu căn

Với nhì biểu thức

mà , ta có; tức là:

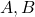
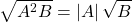
Nếu và thì

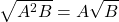
Nếu

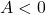
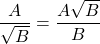
Với những biểu thức nhưng cùng ta có:

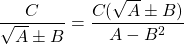
Với các biểu thức cơ mà

và ta có:

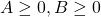
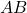
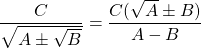
Bài tập: Thực hiện phxay tính chứa căn bậc nhị dưới đây:

1) ;

2)

;

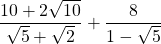
3)

;

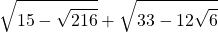
4)

;

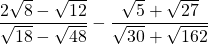
5)

;

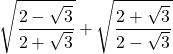
6)

;

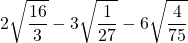
7)

;

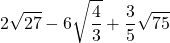
8)

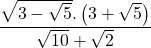
9)

;

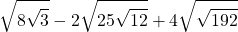
10)

;

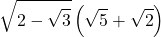
11)

;

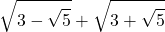
12)

;

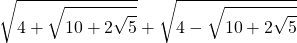
13)

;

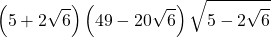
14)

;

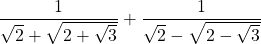
15)

;

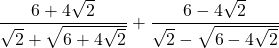
16)

;

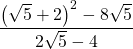
17)

;

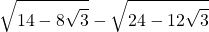
18)

;

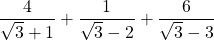
19)

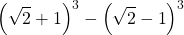
20)

.

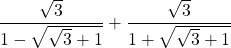
Cách rút gọn biểu thức chứa căn bậc hai

Phương pháp rút ít gọn:

– Phân tích đa thức tử với mẫu thành nhân tử;

– Tìm ĐKXĐ (Nếu bài bác toán thù chưa mang lại ĐKXĐ)

– Rút gọn từng phân thức (nếu được)

– Thực hiện những phxay biến đổi đồng nhất như:

+ Quy đồng (đối với phnghiền cộng trừ) ; nhân ,phân chia.

+ Bỏ ngoặc: bằng biện pháp nhân đơn ; đa thức hoặc sử dụng hằng đẳng thức

+ Thu gọn: cộng, trừ các hạng tử đồng dạng.

+ Phân tích thành nhân tử – rút ít gọn

* Chụ ý: Trong mỗi bài bác toán thù rút ít gọn thường bao gồm những câu thuộc các loại toán: Tính giá bán trị biểu thức; giải Phương trình; bất phương trình; search giá chỉ trị của biến để biểu thức có giá trị nguyên; kiếm tìm giá trị nhỏ nhất ,lớn nhất…Do vậy ta phải áp dụng các Phương pháp giải tương ứng, say mê hợp mang lại từng loại bài bác.

Ví dụ: Cho biểu thức:

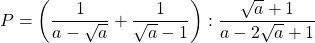
a/ Rút gọn .

b/ Tìm giá trị của để biểu thức có mức giá trị ngulặng.

Giải:

a/ Rút gọn :

– Phân tích:

:fracsqrta+1(sqrta-1)^2" title="Rendered by QuickLaTeX.com" height="46" width="327" style="vertical-align: -20px;">

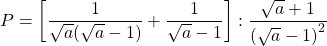
– ĐKXĐ:

0;\sqrta-1 e 0Leftrightarrow a e 1endarray ight." title="Rendered by QuickLaTeX.com" height="43" width="175" style="vertical-align: -17px;">

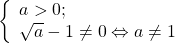
– Quy đồng:

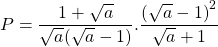
– Rút gọn:

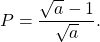
b/ Tìm giá trị của để có mức giá trị nguyên:

– Chia tử mang lại mẫu ta được:

.

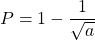
– Lý luận: nguyên

nguyên là ước của 1 là .

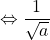
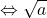
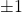
Xem thêm: Chia Sẻ Cách Cài Bluestacks Cho Win Xp, Tải Bluestacks Cho Windows 7/8/10/Xp

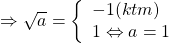
Vậy với

thì biểu thức có giá trị nguyên ổn.

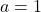
Bài tập rút ít gọn, tính giá trị biểu thức chứa căn lớp 9:

Bài 1: Cho biểu thức

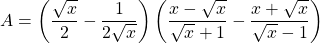
a. Rút gọn biểu thức

;

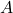
b. Tìm giá trị của để

- 6" title="Rendered by QuickLaTeX.com" height="15" width="60" style="vertical-align: -2px;">.

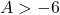
Bài 2: Cho biểu thức

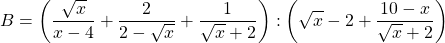
a) Rút ít gọn biểu thức

;

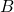
b) Tìm giá bán trị của để

0" title="Rendered by QuickLaTeX.com" height="15" width="46" style="vertical-align: -2px;">.

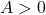
Bài 3: Cho biểu thức:

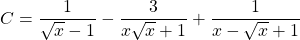
a) Rút ít gọn biểu thức

;

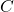
b) Tìm giá trị của để

Rút ít gọn biểu thức:

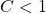
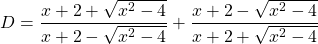
Bài5: Cho các biểu thức:

cùng

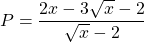
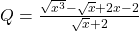
a) Rút ít gọn biểu thức cùng

;

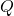
b) Tìm giá chỉ trị của để

.

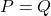
Bài 6: Cho biểu thức:

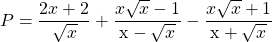
a) Rút gọn biểu thức

b) So sánh với

.

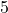
c) Với mọi giá chỉ trị của có tác dụng có nghĩa, chứng minh biểu thức

chỉ nhận đúng một giá chỉ trị nguim.

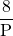
Bài 7: Cho biểu thức:

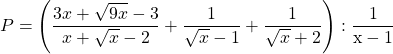
a) Tìm điều kiện để gồm nghĩa, rút gọn biểu thức ;

b) Tìm các số tự nhiên x để

là số tự nhiên;

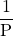
c) Tính giá chỉ trị của với

.

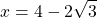
Bài 8: Cho biểu thức :

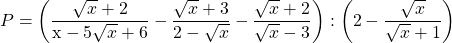
a) Rút gọn biểu thức ;

b/Tìm x để

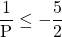
Bài 9: Cho biểu thức :

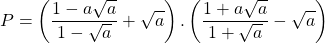
a) Rút gọn

b) Tìm a để

Bài 10: Cho biểu thức:

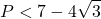
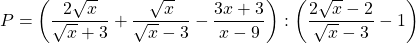
a) Rút ít gọn

b) Tìm x để

Bài 11: Cho biểu thức :

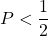
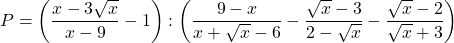
a) Rút gọn

b) Tìm giá trị của để

Bài 12: Cho biểu thức :

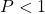
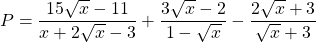
a) Rút ít gọn

b) Tìm những giá bán trị của để

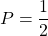
c) Chứng minh

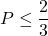
Bài 13: Cho biểu thức:

với m > 0

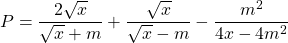
a) Rút gọn

b) Tính theo để

.

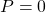
Xem thêm: Phong Cách Nghệ Thuật Tô Hoài Ngắn Gọn, Hay Nhất, Tác Giả Tô Hoài

c) Xác định những giá chỉ trị của để kiếm tìm được ở câu b thoả mãn điều kiện

1" title="Rendered by QuickLaTeX.com" height="14" width="42" style="vertical-align: -2px;">

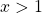
Bài 14: Cho biểu thức :

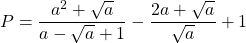
a) Rút gọn

b) Tìm để

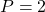
c) Tìm giá chỉ trị nhỏ nhất của ?

Bài 15: Cho biểu thức:

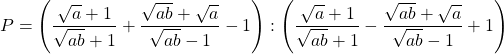
a) Rút ít gọn

b) Tính giá trị của nếu

và

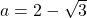
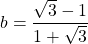
c) Tìm giá trị nhỏ nhất của nếu

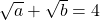
Bài 16: Cho biểu thức:

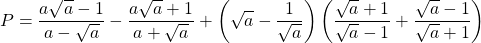
a) Rút ít gọn

b) Với giá bán trị như thế nào của thì

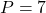
c) Với giá bán trị nào của thì

6" title="Rendered by QuickLaTeX.com" height="14" width="46" style="vertical-align: -2px;">

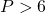
Bài 17: Cho biểu thức:

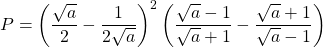
a) Rút gọn

b) Tìm những giá trị của để

: Cho biểu thức:

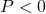
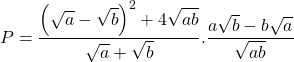
a) Tìm điều kiện để tất cả nghĩa.

b) Rút gọn

c) Tính giá bán trị của Lúc a =

và b =

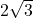
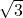
Bài 19: Cho biểu thức:

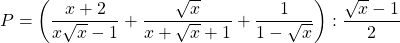
a) Rút ít gọn

b) Chứng minh rằng

0" title="Rendered by QuickLaTeX.com" height="14" width="46" style="vertical-align: -2px;"> với

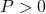
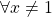
Bài 20: Cho biểu thức :

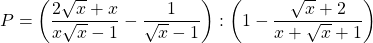
a) Rút gọn

b) Tính

Khi x =

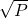
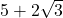
Bài 21: Cho biểu thức:

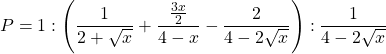
a) Rút gọn

b) Tìm giá trị của để

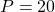
Bài 22: Cho biểu thức :

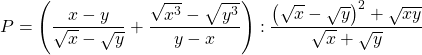
a) Rút gọn

b) Chứng minch P

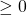
Bài 23: Cho biểu thức :

" title="Rendered by QuickLaTeX.com" height="54" width="597" style="vertical-align: -23px;">

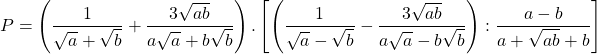
a) Rút gọn

b) Tính Phường khi

cùng

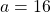
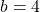
Bài 24: Cho biểu thức:

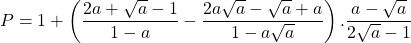
a) Rút ít gọn

b) Cho

tìm kiếm giá chỉ trị của a

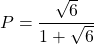
c) Chứng minh rằng

frac23" title="Rendered by QuickLaTeX.com" height="36" width="48" style="vertical-align: -12px;">

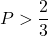
Bài 25: Cho biểu thức:

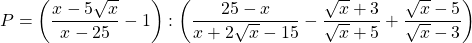
a) Rút ít gọn

b) Với giá chỉ trị như thế nào của thì

: Cho biểu thức:

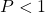
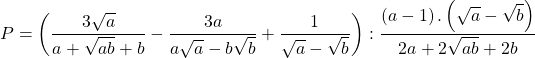
a) Rút gọn

b) Tìm những giá bán trị nguyên ổn của để có mức giá trị nguyên

Bài 27: Cho biểu thức:

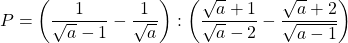
a) Rút ít gọn

b) Tìm giá trị của để

frac16" title="Rendered by QuickLaTeX.com" height="36" width="48" style="vertical-align: -12px;">

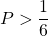
Bài 28: Cho biểu thức:

:fracsqrtx^3+ysqrtx+xsqrty+sqrty^3sqrtx^3y+sqrtxy^3" title="Rendered by QuickLaTeX.com" height="50" width="532" style="vertical-align: -20px;">

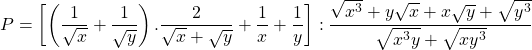
a) Rút gọn

b) Cho

. Xác định để Phường có giá trị nhỏ nhất

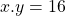
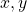
Bài 29: Cho biểu thức:

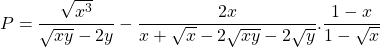
a) Rút ít gọn

b) Tìm tất cả các số nguim dương x để y=625 cùng PBài 30: Cho biểu thức:

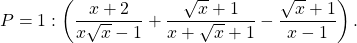
a) Rút gọn

b) So sánh với

Cùng siêng đề:

Cách tìm giá chỉ trị lớn nhất, giá chỉ trị nhỏ nhất của biểu thức sau khoản thời gian rút gọn >>