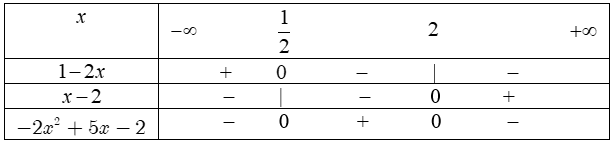
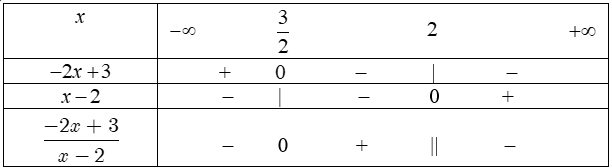
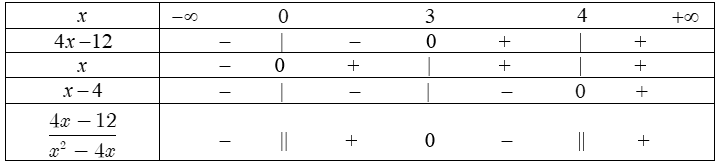
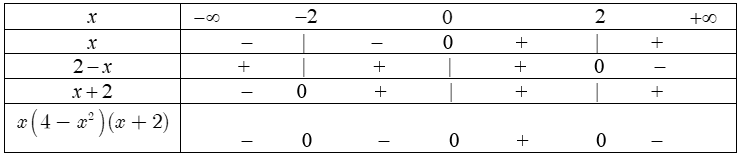
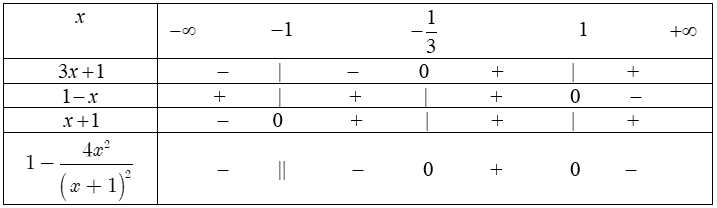
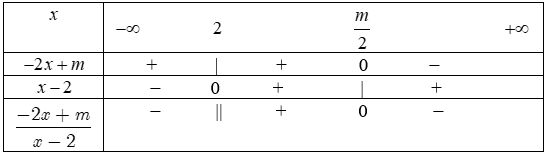
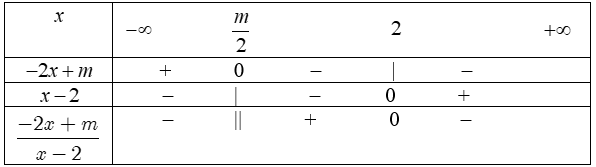
ví dụ như 1. Lập bảng xét dấu các biểu thức sau:
a) $-2x+3.$b) $4x-12.$c) $x^2-4.$d) $-2x^2+5x-2.$a) Ta bao gồm $-2x+3=0$ $ Leftrightarrow x=frac32$, $a=-2Bảng xét dấu: b) Ta tất cả $4x-12=0$ $Leftrightarrow x=3$, $a=4>0.$Bảng xét dấu: c) Ta có:$x^2-4=left( x-2
ight)left( x+2
ight).$$x-2=0$ $ Leftrightarrow x=2.$$x+2=0$ $Leftrightarrow x=-2.$Bảng xét dấu: d) Ta có: $-2x^2+5x-2=0Leftrightarrow left< eginmatrixx=2 \x=frac12 \endmatrix
ight.$Suy ra $-2x^2+5x-2$ $=-2left( x-2
ight)left( x-frac12
ight)$ $=left( x-2
ight)left( 1-2x
ight).$Bảng xét dấu: lấy một ví dụ 2. Lập bảng xét lốt những biểu thức sau:
a) $frac-2x+3x-2.$b) $frac4x-12x^2-4x.$c) $xleft( 4-x^2
ight)(x+2).$d) $1-frac4x^2left( x+1
ight)^2.$a) Bảng xét dấu: b) Ta có: $frac4x – 12x^2 – 4x$ $ = frac4x – 12xleft( x – 4
ight).$Bảng xét dấu: c) Ta có: $xleft( 4 – x^2
ight)(x + 2)$ $ = xleft( 2 – x
ight)left( x + 2
ight)^2.$Bảng xét dấu: d) Ta có: $1 – frac4x^2left( x + 1
ight)^2$ $ = fracleft( x + 1
ight)^2 – 4x^2left( x + 1
ight)^2$ $ = fracleft( 3x + 1
ight)left( 1 – x
ight)left( x + 1
ight)^2.$Bảng xét dấu: lấy một ví dụ 3. Tùy vào $m$ xét dấu các biểu thức sau $frac-2x+mx-2.$a) Ta có:$x-2=0$ $Leftrightarrow x=2.$$-2x+m=0$ $Leftrightarrow x=fracm2.$Trường hòa hợp 1: $fracm2>2$ $Leftrightarrow m>4.$Bảng xét dấu:
Suy ra $frac-2x+mx-2>0$ $Leftrightarrow xin left( 2;fracm2
ight)$ và $frac-2x+mx-2Trường hợp 2: $fracm2=2$ $Leftrightarrow m=4.$Ta gồm $frac-2x+mx-2=frac-2x+2x-2=-2.$Suy ra $frac-2x+mx-2Trường đúng theo 3: $fracm2Bảng xét dấu:
Suy ra $frac-2x+mx-2>0$ $Leftrightarrow xin left( fracm2;2
ight)$ và $frac-2x+mx-2
